Attention Sinks

You’re staring at your attention map. Token 0, the very first one is glowing. Not because it’s important. Not because it’s the subject or the object or the scene. It’s glowing… because it does nothing.
Its value vector? Almost zero.
Its key? Tiny.
And yet, layer after layer, especially the deep ones everyone keeps attending to it.
This makes no sense right? But it kinda does. It actually makes perfect sense.
What transformers really need
Transformers are built on residuals.
\[
\mathbf{x}^{(l+1)} = \mathbf{x}^{(l)} + \mathcal{F}(\mathbf{x}^{(l)})
\]
where \(\mathcal{F}\) is typically → LayerNorm → MultiHeadAttention → LayerNorm → MLP.
For deep stability, long-sequence coherence, and representation preservation, the model must be able to learn:
\[
\mathcal{F}(\mathbf{x}^{(l)}) \approx 0
\]
But Attention is not naturally identity-friendly
\[
\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left( \frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d_k}} \right) \mathbf{V}
\]
it always produces a convex combination of value vectors a weighted average, not a copy. Even if Q=K=V , attention redistributes information it does not preserve. So Even if you want to output zero you can’t just “turn off” attention. Softmax forces you to spread probability mass over all tokens.
And if you’re dumb enough to attend to a token with a big value? Congrats, you just ruined your perfect representation.
So how does a transformer learn to output ≈0 when needed? Attention Sinks!
The Model’s Solution: Invent a Token That Outputs Zero
So the model picks a token usually token 0 and trains it to have two properties:
Property 1: Value Vector ≈ 0
\[
\|\mathbf{v}_0\|_2 \approx 0
\]
So when other tokens attend to it contribution to output is near zero.
\[
A_{i0} \cdot \mathbf{v}_0 \approx 0
\]
Now Even if \(A_{i0} = 0.9\), if \(\mathbf{v}_0 \approx 0\) , you get almost no change. this lets the model approximate :
\[
\text{Attention}(x)_i ≈ 0 → output ≈ x_i → identity
\]
But you can’t have everyone attending to token 0 all the time. That would break everything.
Property 2:
the model trains \(k_{0}\) to be :
- Low norm: \(\|k_0\|_2\) is small → harder to get high attention scores accidentally
- Orthogonal or negatively correlated with other keys so normal queries (attending to content) get low or negative dot products
To prevent accidental attention to the sink, the model learns: \[ k_s^\top k_j \approx 0 \quad \forall j \neq s \] where \( \|k_s\| is \text{ small} \) why? Consider the attention score (if vectors are row, this might create confusion towards the end so from now on vectors are treated as columns similar to how pytorch does it): \[ s_{ij} = q_i^\top k_j / \sqrt{d} \] If \(k_s\) is orthogonal to all other \(k_j\), then \(q_i\) must be explicitly aligned with \(k_s\) to produce high \(s_{is}\) and random or content-directed \(q_i\) will have \(s_{is} \approx 0\) which when combined with small \(\|k_s\|\), this ensures low baseline attention to sink and high only when intentionally triggered. So basically :
- \(q_i\) aligns with \(k_s\) → attend to sink → output ≈ 0 → identity.
- \(q_i\) aligns with content keys → attend to content → update.
Observations in Experiments
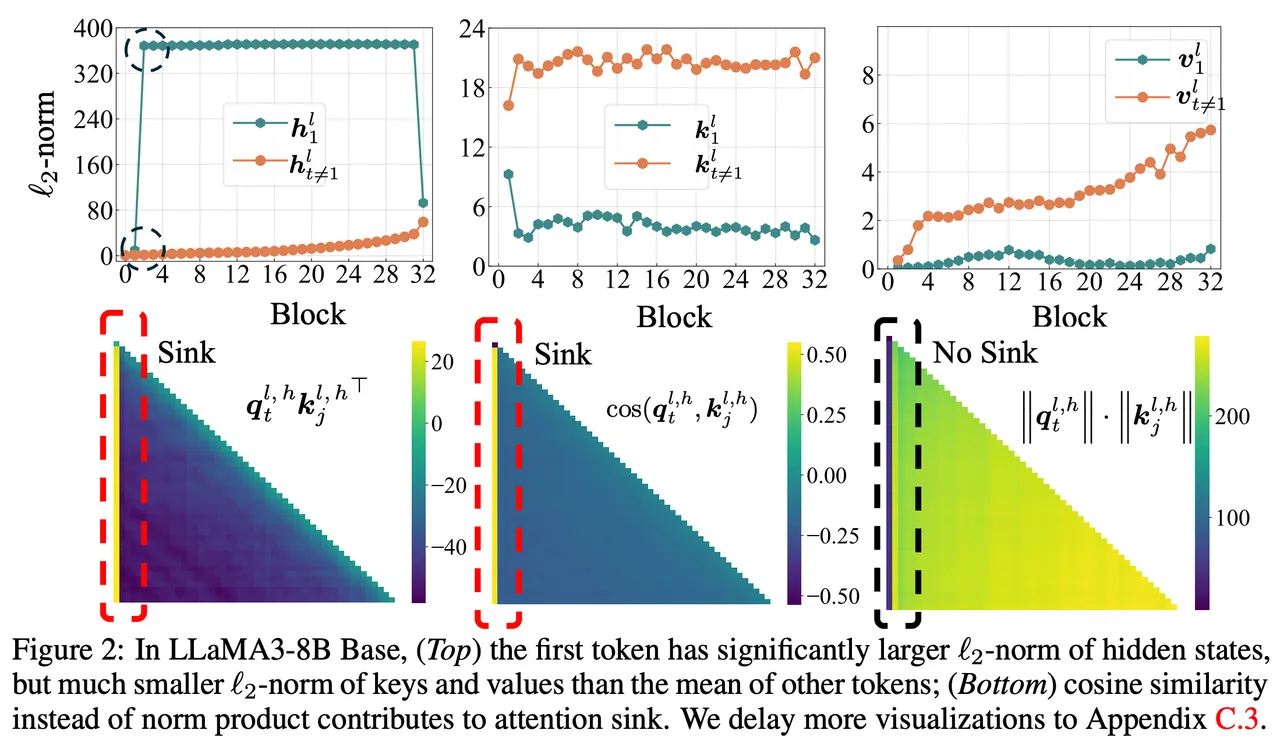
This very plot comes from https://arxiv.org/pdf/2410.10782
Value Norm Plot (First row, third column in above figures)
- X-axis: token index
- Y-axis: L2 norm of value vector \(\|\mathbf{v}_j\|_2\)
- Observation: token 0 is near zero. Others are larger. which confirms: attending to token 0 ≈ no change.
- Y-axis: \(\|\mathbf{k}_j\|_2\)
- Observation: token 0’s key norm is small.
- Confirms: only strong, deliberate alignment can trigger attention.
- Y-axis: cos\( ( \mathbf{k}_0, \mathbf{k}_j) \) for \( j \ne 0 \)
- Observation: values near 0 or negative.
- Confirms: sink key lives in isolated subspace — no interference.
- X-axis: layer index
- Y-axis: mean attention weight to token 0
- Observation: increases in deeper layers. which confirms: used for stabilization after representations saturate.
The plots are for LLaMA3-8B, in the next blog (hopefully soon) I'll explore sliding window on video models specially WAN2.2 while taking attn sinks in account.
Why This Gets Worse in Long Sequences — Attention Dilution
Let's understand the models attention entropy, let's define the attention distribution over tokens for query \(i\) - \( p_i(j) = \alpha_{ij} \) the entropy of this distribution is :
\[
H(p_i) = -\sum_j p_i(j) \log p_i(j)
\]
In long sequences (wher \(N\) is large), if attention is uniformly diffused \(H(p_i) \approx \log N\) which means High entropy → attention spread thin → no token receives strong focus. This is what attention dilation is pretty much.
Now if we recall, to approximate identity the model needs \(\alpha_{is} \approx 1\) (think of the softmax formula when you read this).
\[
\alpha_{is} = \frac{\exp(q_i k_s^\top / \sqrt{d})}{\sum_{m=1}^N \exp(q_i k_m^\top / \sqrt{d})}
\]
But in long sequences, the softmax denominator grows denoted by \(Z_i\). Here as \(N\) increases, \(Z_i\) increases → all \( \alpha_{ij}\) shrink unless \(q_i k_j^\top\) is very large.
\[
Z_i = \sum_{m=1}^N \exp(q_i k_m^\top / \sqrt{d})
\]
So to make \( \alpha_{is} \approx 1 \), the model must make:
\[
q_i k_s^\top \gg q_i k_j^\top \quad \forall j \neq s
\]
But if \(k_s\) is low-norm and orthogonal, this requires \(q_i\) to be extremely aligned, which is expensive and unstable. So what happens ?
- The model amplifies sink attention even more to compensate for dilution.
- Sink weights become more extreme in long sequences.
- Token 0 receives disproportionately higher attention as \(N\) grows.
Sink Amplification
Assume \(k_s\) is orthogonal to all other keys: \(k_s^\top k_j = 0\), \(\|k_s\| = \epsilon\) is small, all other \( k_j\) live in a subspace orthogonal to \(k_s\), with \(\|k_j\| \approx 1\) and \(q_i\) is a unit vector for simplicity (refer this) then: \[ q_i k_s^\top = \epsilon \cos \theta_s \] \[ q_i k_j^\top = \cos \theta_j \quad \text{(for j ≠ s)} \] Softmax attention sink: \[ \alpha_{is} = \frac{\exp(\epsilon \cos \theta_s / \sqrt{d})}{\exp(\epsilon \cos \theta_s / \sqrt{d}) + \sum_{j \neq s} \exp(\cos \theta_j / \sqrt{d})} \] As \(N\) grows, the denominator’s sum grows → \(\alpha_{is}\) shrinks. To keep \(\alpha_{is} \approx 1\), the model must make \(\cos \theta_s \approx 1 → q_i\) fully aligned with \(k_s\) and make \( \cos \theta_j \approx -1\) or 0 for all other \(j\) → suppress all other keys. This is computationally expensive and geometrically fragile. Instead the model takes and easy way out :
- In early layers: spread attention, build features.
- In deep layers: collapse attention to sink → force identity → survive dilution.
Dimentional Waste and Capacity Loss
The sink burns two representation slots One key dimension: forced into orthogonal subspace → can’t encode content and one value dimension: forced toward zero → can’t contribute signal. In a model with d_model = 1024, and N = 32,768 tokens, you’re wasting:
- 1024 key dimensions
- 1024 value dimensions
Gating at output
I would highly recomend reading this little piece on gating and if you are still here this is my take on it.
introduce scalar gate \(g_i \in [0,1]\) per token:
\[
x_{l+1} = x_l + g_i \cdot \text{Attn}(x_l)_i
\]
Now if \(g_i = 0\) → \(output = x_l\) → identity, if \(g_i = 1\) → full attention update and If \(g_i = 0.3\) → partial update.
No need for \(v_s\) ≈ 0. No need for orthogonal \(k_s\). No attention dilution problem. The model learns \(g_i\) via a tiny MLP:
\[
g_i = \sigma(W_g x_l[i] + b_g)
\]
which costs 1024 * 1 parameters per layer → negligible. Qwen’s experiments confirm: only G1 gating kills the sink because only G1 can explicitly nullify attention output. All other gating positions (after MLP, etc.) can’t force \(F_l(x) = 0\) since the attention already fired.
To Conclude
- Transformers require context-aware identity for residual stability
- Softmax attention cannot output zero due to convex combination constraint.
- Model approximates zero in order to learn token with \(v_s\) ≈ 0.
- Isolates \(k_s\) → orthogonal, low-norm means clean switching.
- In long sequences, attention dilutes in turn model amplifies sink to compensate.
- This wastes dimensions and destabilizes training.
- Gating at attention output (G1) allows explicit zeroing which eliminates sink.
Now since the whole point of this blog was to explore Attention Sinks in Video Diffusion models (in the next part), here's some experiments I'm currently doing with WAN2.2 in order to account for attn sinks.
Attention Sinks and Video Diffusion Models
My assumption is to see a couple of patches at the start to show the sink behaviours since "Any sufficiently trained transformer that uses softmax will exhibit attention sink." now in order to generate huge videos everyone uses sliding window attention and let's be real, you're not retraining WAN from scratch nor adding gates. The sink is inevitable might as well make it useful.- What if you designed your sliding window to respect the sink and not ignore it?
- What if every local window always includes token 0 or patch 0 or whatever?
- What if the sink became your anchor point for temporal coherence, while sliding attention handles motion, texture, lighting?
- https://quilted-agreement-28c.notion.site/Why-Does-Attention-Sink-Occur-21568e7f8199809586b8e05cc97b90a9#21568e7f81998007a2c7ece3c02c5730
- https://x.com/zmkzmkz/status/1917547438258450674
- https://www.youtube.com/watch?v=PKYvAc9UZhk
- https://github.com/sail-sg/Attention-Sink